Ramanujan, el indio pobre y autodidacta que dejó un legado eterno en el mundo de las matemáticas


Este 26 de abril se celebra el centenario de la muerte del matemático indio Srinivasa Ramanujan (1887-1920). Dentro de lo desconocidas que son las figuras destacadas de las matemáticas por el gran público, se podría decir que Ramanujan es un matemático conocido. Tomando prestada una frase de Antonio Córdoba, su popularidad se debe a que está cargado de “un halo de romanticismo”. No en vano se le ha dedicado una película de mediano presupuesto (basada en la biografía de R. Kanigel) y al menos otra de menor difusión. A esto se suma un aire misterioso entre los expertos que todavía hoy se preguntan cómo llegó a muchos de sus resultados.
Ramanujan nació en Erode en 1887 y pasó casi toda su vida en Kumbakonam, en su India natal. Tras destacar en la escuela, tuvo la posibilidad de acceder a una educación superior y universitaria con una beca en 1904 y 1906 pero, en parte por su excesiva dedicación a las matemáticas y en parte por su salud, la perdió (en los exámenes solo aprobó las matemáticas). Investigó aislado sin casi contacto con el trabajo de otros matemáticos entre 1903 y 1910. En 1912 consiguió un empleo como oficinista en Madrás (hoy Chennai). Sus notables aptitudes le dieron cierta fama y se le aconsejó entrar en contacto con matemáticos ingleses, ya que entonces la India estaba bajo control británico. Después de tres intentos fallidos, en 1913 escribió una carta al profesor de la Universidad de Cambridge Godfrey H. Hardy quien quedó tan impresionado con algunos de sus hallazgos que lo invitó a visitar su institución. Después de vencer dudas y objeciones familiares, Ramanujan viajó a la metrópoli en 1914 y en Cambridge consiguió lo que hoy llamaríamos un doctorado. Desafortunadamente a finales de 1916 cayó muy enfermo y, tras acabar la Primera Guerra Mundial, volvió a la India en 1919 donde su gravosa enfermedad lo siguió atormentando hasta su muerte, el 26 de abril de 1920, cuando contaba 32 años.
La investigación que Ramanujan realizó fuera de Inglaterra es misteriosa, sobre todo la anterior a Cambridge (la posterior, cuando ya estaba muy enfermo, era incluso casi desconocida hasta que en 1976 George E. Andrews descubrió más de cien páginas manuscritas que se han dado en llamar “El cuaderno perdido”). En su trabajo solitario escribió miles de resultados matemáticos en tres cuadernos pero debido al precio del papel y a que trabajaba en pizarra (que todavía se conserva) solo apuntó los enunciados y no las pruebas. Estos cuadernos eran para uso privado y seguramente pensó que podría incorporar las demostraciones cuando tuviera ocasión de publicarlas. En Cambridge, donde aprendió el rigor requerido en matemáticas, escribió en 1914 a un amigo que planeaba hacerlo cuando acabase la guerra (entonces se pensaba que sería breve) pero aquello nunca sucedió. El gran misterio es qué técnicas usó para obtener muchos de sus resultados con las importantes lagunas de su formación autodidacta.
Tras la muerte de Ramanujan, George N. Watson y Bertram M. Wilson emprendieron la tarea de dar pruebas a los enunciados de los cuadernos. Bruce C. Berndt ha liderado y concluido dicha tarea y tras la titánica labor de toda una vida ha publicado cinco tomos (sin contar el “cuaderno perdido”) titulados “Ramanujan’s notebooks”, el último, en 1998. Sin embargo esta obra monumental no aclara del todo el misterio, son las pruebas que se han sabido dar de los resultados de Ramanujan pero en muchos casos no coinciden con las que pudo dar él con sus conocimientos cuando trabajaba aislado. En 1988, Berndt afirmó: “El enigma del proceso creativo de Ramanujan está todavía cubierto por un telón que apenas ha sido levantado”. Aunque hoy intuimos algo más, el misterio perdura.
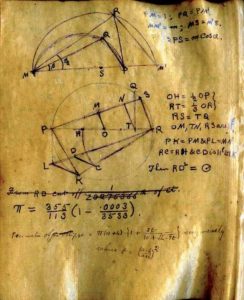

Uno de los manuscritos de Ramanujan.
A menudo los resultados de sus cuadernos están expresados como evaluaciones de series infinitas o identidades entre ellas, demasiado complicadas para glosarlas aquí. Por ello trataré de acercar al lector al misterio de Ramanujan a través de uno de sus resultados más elementales, que no le hace justicia. Consideremos las raíces cúbicas de los cosenos de 800, 400 y 200, sumemos las dos primeras y restemos la tercera elevando el resultado final al cubo y sumando 3. El número que se obtiene es 3,1201… que Ramanujan expresa con una fórmula muy sencilla con un solo radical: 3/2 por la raíz cúbica de 9. Sí, esto es algo anecdótico pero el lector con gusto matemático se preguntará dónde está el truco, por qué ese cálculo tan complicado se simplifica y cómo alguien puede imaginarlo. En otros hallazgos que requieren matemáticas más avanzadas, todavía hoy nos preguntamos cómo los obtuvo Ramanujan.
La genialidad es una característica tan especial que es muy fácil añadir incomprendido como si fuera epíteto y pasar del genio al mito. Quizá en las bellas artes, con gustos y modas más cambiantes, se pueda mencionar un número de genios poco valorados en su época pero ciertamente esto no es lo común en la historia de las matemáticas. En particular no es el caso de Ramanujan y lo es menos teniendo en cuenta las carencias en sus conocimientos y sus escasos medios. Por dar algunos datos, en vida fue elegido “Fellow of the Royal Society” y “Fellow of the Trinity College” (dos excelsos honores insólitos entonces para un indio), publicó casi 40 trabajos en revistas de investigación, cuando volvió a la India dos artículos periodísticos acreditaron las hipérboles “en algunos aspectos el matemático más notable del mundo” y “el mayor genio desde Newton”, sus ‘Collected Papers’ fueron publicados por Cambridge University Press siete años después de su muerte y tras ella hubo una cantidad nada desdeñable de artículos de investigación relacionados con su obra. Un caudal que cien años después llega hasta nuestros días.
elconfidencial








